The QR Algorithm and Modified Gram-Schmidt¶
Preamble: Run the cells below to import the necessary Python packages
This notebook created by William Gilpin. Consult the course website for all content and GitHub repository for raw files and runnable online code.
import numpy as np
# Wipe all outputs from this notebook
# from IPython.display import Image, clear_output
# clear_output(True)
# Import local plotting functions and in-notebook display functions
import matplotlib.pyplot as plt
%matplotlib inline
Eigensystems¶
The "natural" coordinate system for a matrix
Hermitian matrices: can always rotate a collection of vectors, but the eigenspectrum gives us the dominant directions and scales associated with a bundle
Dynamical systems view: A "blob" of initial conditions gets anisotropically stretched along the eigendirections at different rates
Eigenvalues are invariant to rotations (ie, multiplication by an orthonormal matrix)
Finding eigenspectra is difficult for large matrices¶
Suppose we are given a square matrix $A \in \mathbb{R}^{N \times N}$. How can we find the eigenvalues and eigenvectors of this matrix numerically? The schoolyard method for performing this calculation consists of first solving the characteristic equation for the eigenvalues $\lambda$ such that $$ \det(A - \lambda \mathbb I) = 0. $$ Calculation of the determinant has runtime complexity $\sim N^3$, making computation of the characteristic polynomial itself no harder than matrix multiplication. However, the hard part is factoring the characteristic equation into a form amenable to finding the eigenvalues, $(\lambda - \lambda_1)(\lambda - \lambda_2)...(\lambda - \lambda_N) = 0$. Since the polynomial has order $\mathcal{O}(\lambda^N)$, at large $N$, it often becomes impractical to use numerical root-finding to solve the eigenvalue problem using schoolyard methods.
Iterative linear algebra methods¶
Pros¶
- More predictable time cost (complexity input agnostic)
- Easier to control precision/runtime
- Potentially faster in cases with fast convergence
- Can exploit sparsity
Cons¶
- Indirect and approximate, but might have epsilon guarantees (e.g. Arnoldi methods)
- Not guaranteed to converge
- Bad starting conditions or ill-conditioning can lead to a large prefactor in the runtime to reach a given target accuracy
QR Factorization and Gram Schmidt orthogonalization¶
We saw before that classical schoolyard methods for matrix inversion via Gauss-Jordan elimination could be summarized as a single matrix, the $L^{-1}$ of LU factorization.
For orthogonalization, instead of Gauss-Jordan elimination we use Gram-Schmidt orthogonalization to build up an orthonormal basis from a bundle of vectors. Like Gauss-Jordan, this process can be summarized as a matrix product, the QR factorization $A = QR$.
We therefore expect a runtime complexity of $\mathcal{O}(N^3)$ for QR factorization.
The Press textbook describes other orthogonalization methods (Givens rotations, Householder triangularization)
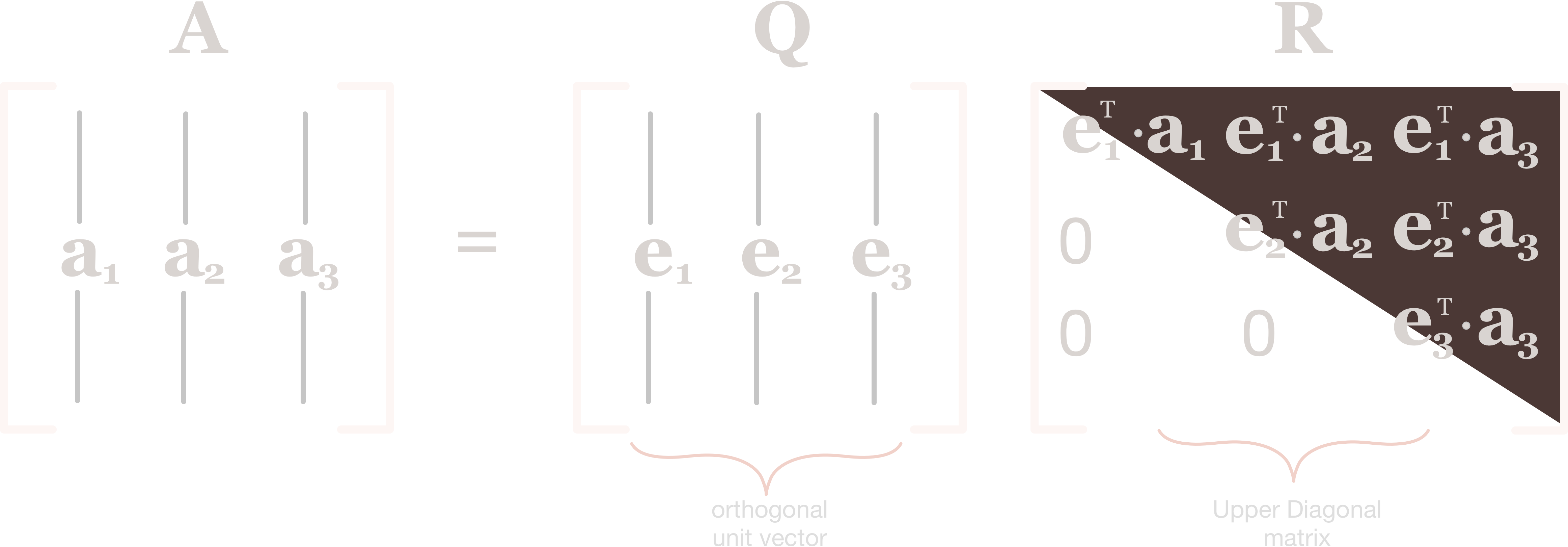
Image from Source
To illustrate the QR algorithm, we start by picking two vectors and orthogonalizing them.
np.random.seed(10)
vec1, vec2 = np.random.rand(2), np.random.rand(2)
# bounds = np.array([vec1, vec2]).max(axis=0) + 0.5
## draw the vectors with arrowheads
plt.figure(figsize=(6, 6))
plt.quiver(0, 0, vec1[0], vec1[1], angles='xy', scale_units='xy', scale=1, color='r')
plt.quiver(0, 0, vec2[0], vec2[1], angles='xy', scale_units='xy', scale=1, color='b')
plt.xlim(-1, 1)
plt.ylim(-1, 1)
# # # Project vec2 onto vec1, and then scale vec1 by the ratio of the projection to the length of vec1
vec2_proj_onto_vec1 = np.dot(vec2, vec1) / np.dot(vec1, vec1) * vec1
# # # Subtract the projection from vec2
vec2_orth = vec2 - vec2_proj_onto_vec1
# plt.figure(figsize=(6, 6))
# # Draw the projection, add a small offset to avoid overlapping vectors
plt.quiver(
0, 1e-2, vec2_proj_onto_vec1[0], vec2_proj_onto_vec1[1] + 1e-2,
angles='xy', scale_units='xy', scale=1, color='b', alpha=0.5)
# # # Draw the orthogonalized vector
plt.quiver(0, 0, vec1[0], vec1[1], angles='xy', scale_units='xy', scale=1, color='r')
plt.quiver(0, 0, vec2_orth[0], vec2_orth[1], angles='xy', scale_units='xy', scale=1, color='b')
plt.xlim(-1, 1)
plt.ylim(-1, 1)
(-1.0, 1.0)
What if we wanted to invert this process? We can walk through the steps of the Gram-Schmidt process
$[\mathbf{v}_1, \mathbf{v}_2]$ are our starting vectors, and $[\mathbf{q}_1, \mathbf{q}_2]$ are our orthogonalized vectors.
We can recover the first vector by writing
$$ \mathbf{v}_1 = \mathbf{q}_1 (\mathbf{v}_1 \cdot \mathbf{q}_1) + \mathbf{q}_2 (0) $$
We can recover the second vector by writing
$$ \mathbf{v}_2 = \mathbf{q}_1 (\mathbf{v}_2 \cdot \mathbf{q}_1) + \mathbf{q}_2 (\mathbf{v}_2 \cdot \mathbf{q}_2) $$
We can therefore store the parenthetical scalar terms in their own matrix, $R$, and write the above equations as
$$ \begin{bmatrix} \mathbf{v}_1 & \mathbf{v}_2 \end{bmatrix} = \begin{bmatrix} \mathbf{q}_1 & \mathbf{q}_2 \end{bmatrix} \begin{bmatrix} R_{11} & R_{12} \\ 0 & R_{22} \end{bmatrix} $$ where $R_{ij} = \mathbf{v}_i \cdot \mathbf{q}_j$.
# Create a matrix with vec1 and vec2 as columns
A = np.array([vec1, vec2]).T
# Normalize the "first" vector to get q1, the first unit vector
vec1_norm = np.linalg.norm(vec1)
q1 = vec1 / vec1_norm
# Normalize the orthogonal vector to get q2
vec2_orth_norm = np.linalg.norm(vec2_orth)
q2 = vec2_orth / vec2_orth_norm
# Construct the Q matrix, which is the matrix of unit vectors. The first column
# points in the same direction as vec1
Q = np.array([q1, q2]).T
# Construct the R matrix
R = np.zeros((2, 2))
R[0, 0] = vec1_norm
R[0, 1] = np.dot(q1, vec2)
R[1, 1] = vec2_orth_norm
# R is the matrix of projections onto the previous vectors
# R = np.array([[np.dot(vec1, vec1), np.dot(vec1, vec2)], [0, np.dot(vec2_orth, vec2_orth)]])
# Check that Q and R recreate A
print('Q = \n', Q)
print('R = \n', R)
print('Q @ R = \n', Q @ R)
print('A = \n', A)
print(np.allclose(A, Q @ R))
Q = [[ 0.99963827 -0.02689471] [ 0.02689471 0.99963827]] R = [[0.77159975 0.65355789] [0. 0.73149124]] Q @ R = [[0.77132064 0.63364823] [0.02075195 0.74880388]] A = [[0.77132064 0.63364823] [0.02075195 0.74880388]] True
For non-square matrices, we might append extra orthogonal columns to $Q$ and zeros to $R$, so that $Q$ now represents a full-rank matrix with rowsspace spanning its full columnspace
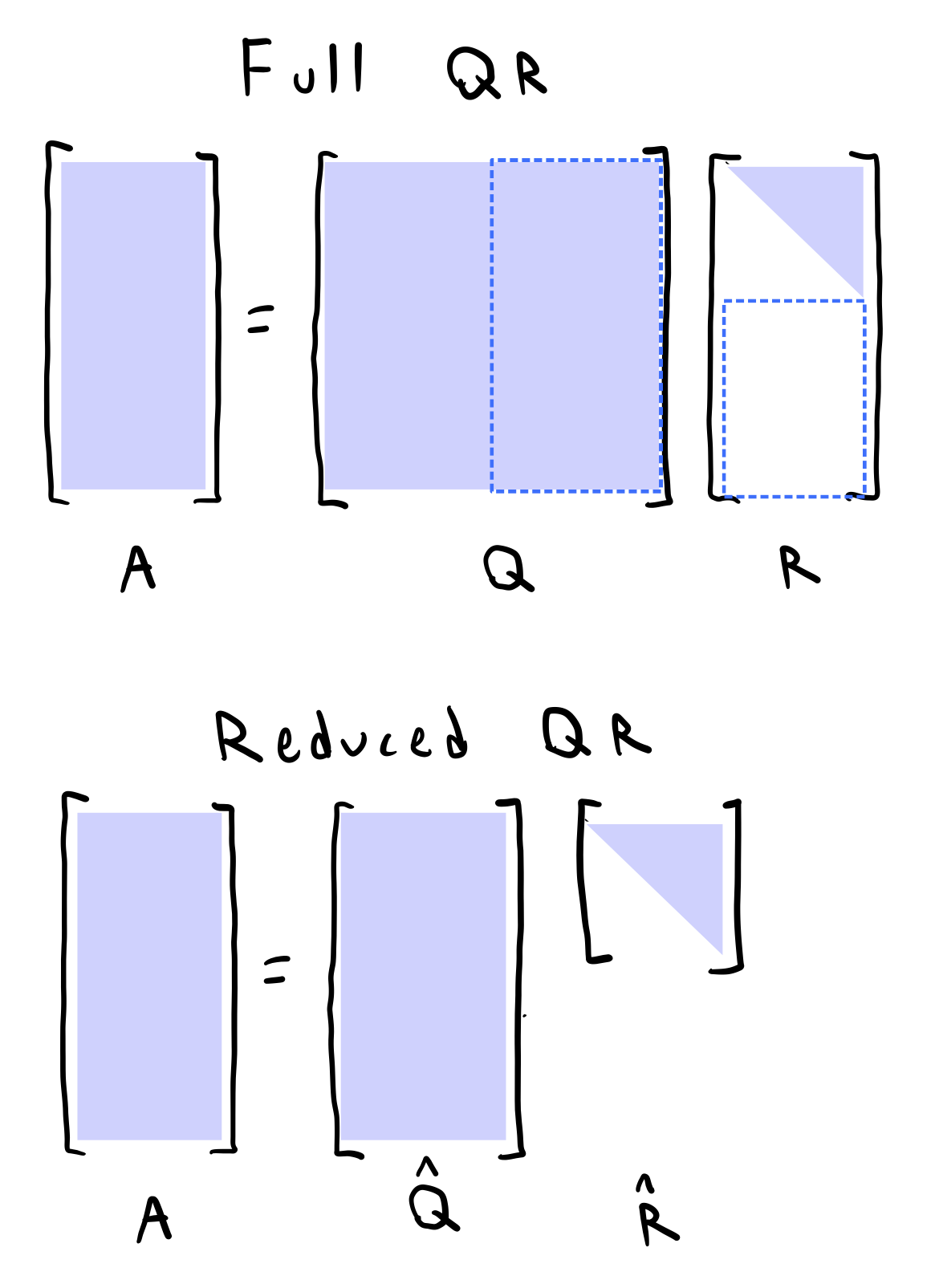
The steps of the Gram-Schmidt algorithm are as follows:
- Pick a column vector $\mathbf{v}_1$ from the matrix $A$ and normalize it to have unit length. This will be the first column of the matrix $Q$.
- Move to the next column vector $\mathbf{v}_2$ of $A$. Subtract the projection of $\mathbf{v}_2$ onto $\mathbf{q}_1$ from $\mathbf{v}_2$. Normalize the resulting vector to get the second column of $Q$.
- Move to the third column vector $\mathbf{v}_3$ of $A$. Subtract the projection of $\mathbf{v}_3$ onto $\mathbf{q}_1$ and the projection of $\mathbf{v}_3$ onto $\mathbf{q}_2$. Normalize the resulting vector to get the third column of $Q$.
- Repeat steps 1 and 2 for the remaining columns of $A$ to build the full $Q$ and $R$ matrices.
So. in traditional Gram-Schmidt, once we've passed a column and normalized it, we never touch it again. All future columns are orthogonalized with respect to the columns we've already processed. By the time we get to the last column of an $N \times N$ matrix, we need to subtract $N-1$ projections from it to orthogonalize it.
def qr_factorization(X):
"""
Compute the QR factorization of a square matrix using iterative Gram-Schmidt
orthonormalization.
Args:
X (numpy.ndarray): A square matrix.
Returns:
Q (numpy.ndarray): An orthonormal matrix.
R (numpy.ndarray): The upper triangular matrix.
"""
X = X.T # want first index to be the column index (for convenience)
q, r = np.zeros(X.shape), np.zeros(X.shape) # preallocate Q and R
## Pick first vector as the "pivot" and normalize it
q[0] = X[0] / np.linalg.norm(X[0])
## Project rest of the vectors onto the pivot
r[0] = X @ q[0]
for i in range(1, X.shape[0]):
## Orthogonalize the vector by subtracting off the projections onto all previous vectors
q[i] = X[i] - np.sum(np.dot(X[i], q[:i].T) * q[:i].T, axis=-1)
## Normalize the orthogonalized vector
q[i] /= np.linalg.norm(q[i])
## Update the upper triangular matrix R
r[i, i:] = X[i:] @ q[i]
q = q.T # because we wrote into rows instead of columns
return q, r
A = np.random.normal(size=(10, 10))
q, r = qr_factorization(A)
np.allclose(A, q @ r)
True
Iterative eigenspectrum calculation via the QR eigenvalue method¶
How do we get the eigenspectrum of a matrix using QR factorization? Recall that rotating a matrix does not change its eigenvalues. The orthogonal basis $Q$ returned by QR factorization is a rotation matrix, and so the eigenvalues of $A$ are the same as the eigenvalues of $R = Q^T A Q$. Recall that, for orthogonal matrices, $Q^T = Q^{-1}$.
We can therefore repeatedly rotate the matrix $A$ using QR factorization until it becomes diagonal, in which case the diagonal entries are the eigenvalues of $A$.
We therefore have an iterative algorithm for computing the eigenvalues and eigenvectors of a symmetric matrix $A$, $$ Q_k, R_k \leftarrow \text{QR}(A_k) $$ $$ A_{k+1} \leftarrow R_k Q_k $$ $$ T_{k+1} \leftarrow T_k Q_k $$ where $T_0 = \mathbb{I}$ and $A_k = Q_k R_k$ via QR factorization. This matrix tracks the combined cumulative rotation of all of the $Q_k$ matrices, and we need it to get the eigenvectors of $A$ in addition to the eigenvalues.
Why does this work?¶
Recall that $R$ is a triangular matrix with non-zero entries given by $\mathbf{v}_i \cdot \mathbf{q}_j$. The rotations associated with a given intermediate $Q_k$ gradually push the off-diagonal elements of $R$ to zero.
Our implementation¶
Here, we are going to implement the QR algorithm in Python. Note that numpy, as in other languages, uses row, column format for indexing. Since we often interpret a matrix as an array of column vectors, selecting the ith column vector of a matrix a has the form a[:, i]. By convention, eigenvectors are returned in a format where the columns are eigenvectors, and so we select individual eigenvectors along the second axis.
We can break our implementation into several stages:
- Implementing QR factorization. We can use either the Gram-Schmidt algorithm or Householder reflections to compute the QR factorization.
- Computing an eigensystem via repeated QR factorization and transformation
class QREigendecomposition:
"""
A numpy implementation of the QR eigenvalue algorithm for symmetric matrices
Attributes:
eigenvalues (numpy.ndarray): The eigenvalues of the matrix.
eigenvectors (numpy.ndarray): The eigenvectors of the matrix, stored as columns.
store_intermediate (bool): Whether to store the intermediate matrices.
"""
def __init__(self, store_intermediate=False):
self.eigenvalues = None
self.eigenvectors = None
self.store_intermediate = store_intermediate
def qr_factorization(self, X):
"""
Compute the QR factorization of a square matrix using gram-schmidt
orthonormalization.
Args:
X (numpy.ndarray): A square matrix.
Returns:
Q (numpy.ndarray): An orthonormal matrix.
R (numpy.ndarray): The upper triangular matrix.
"""
X = X.T # want first index to be the column index (for convenience)
q, r = np.zeros(X.shape), np.zeros(X.shape) # preallocate
q[0] = X[0] / np.linalg.norm(X[0])
r[0] = X @ q[0]
for i in range(1, X.shape[0]):
q[i] = X[i] - np.sum(np.dot(X[i], q[:i].T) * q[:i].T, axis=-1)
q[i] /= np.linalg.norm(q[i])
## Update the upper triangular matrix R
r[i, i:] = X[i:] @ q[i]
q = q.T # because we took transpose beforehand for easier indexing
return q, r
def find_eigensystem(self, X, max_iter=2000, tol=1e-6):
"""
Find the eigenvalues and eigenvectors of a matrix
Args:
X (numpy.ndarray): A square matrix.
max_iter (int): The maximum number of iterations to perform.
tol (float): The tolerance for convergence.
Returns:
eigenvalues (numpy.ndarray): The eigenvalues of the matrix.
"""
prev = np.copy(X)
tq = np.identity(X.shape[0])
if self.store_intermediate: self.intermediate = [np.copy(X)]
for i in range(max_iter):
q, r = self.qr_factorization(X)
X = r @ q # q^-1 x q
# np.matmul(r, q)
# np.dot(r.T, q)
# np.einsum('ij,jk->ik', r, q)
tq = tq @ q # accumulate the eigenvector matrix
if self.store_intermediate: self.intermediate.append(np.copy(X))
## Check for convergence and stop early if converged
if np.linalg.norm(X - prev) < tol:
break
prev = np.copy(X)
eigenvalues, eigenvectors = np.diag(X), tq
sort_inds = np.argsort(eigenvalues)
eigenvalues, eigenvectors = eigenvalues[sort_inds], eigenvectors[:, sort_inds]
self.eigenvalues, self.eigenvectors = eigenvalues, eigenvectors
return eigenvalues, eigenvectors
a = np.random.random((10, 10))
a = a @ a.T # ensure symmetric
model = QREigendecomposition(store_intermediate=True)
eigenvalues, eigenvectors = model.find_eigensystem(a)
plt.figure()
plt.plot(eigenvalues)
plt.title("Eigenvalues from QR method")
plt.figure()
plt.plot(np.linalg.eigh(a)[0])
plt.title("Eigenvalues from numpy")
print(np.allclose(eigenvalues, np.linalg.eigh(a)[0]))
True
all_r = [model.qr_factorization(X)[1] for X in model.intermediate]
plt.imshow(all_r[-1])
<matplotlib.image.AxesImage at 0x10f7616d0>
Why does this algorithm work?¶
For a full-rank matrix $A$, we can always find an orthonormal matrix via QR factorization using a method such as Gram-Schmidt orthonormalization. The $Q$ matrix represents the basis, and the upper-triangular $R$ matrix represents the weights necessary to project the original matrix $A$ into the orthogonal basis.
Recall that the eigenvalues of a matrix are invariant to changes in basis, and so the $Q$ matrix essentially acts like a rotation (technically called the "Givens rotations"). When we perform the transformation $R Q$, we are essentially calculating $Q^{-1} A Q$ (you can use some linear algebra tricks to confirm this). This essentially represents a change of basis, which gradually aligns the columns of $A$ with the eigenvectors, resulting in an upper-triangular form where we can just read the eigenvalues off the diagonal.
Moreover, because a composition of rotations is still a rotation, but keeping track of the net rotation in the matrix $T_k$, we can immediately read off the eigenbasis for the system.
For a more technical description of this algorithm, as well as explicit definition of the Gram-Schmidt orthonormalization process, we refer to Chapter 11 of William Press's Numerical Recipes textbook, as well as these lecture notes by Peter Arbenz
What to do next¶
- Instead of using Gram-Schmidt, try implementing orthonormalization using Householder reflections
- It's possible to generalize the QR algorithm to work for non-symmetric matrices with complex eigenvalues. However, this implementation is pretty subtle. A good discussion is provided in the Watkins textbook
# Let's do a simple unit test to make sure that our class is working as expected
import unittest
class TestQR(unittest.TestCase):
def test_factorization(self):
"""
Test that the QR factorization is correct
"""
np.random.seed(0)
a = np.random.random((20, 20))
model = QREigendecomposition()
q, r = model.qr_factorization(a)
self.assertTrue(np.allclose(a, q @ r), "QR factorization failed")
def test_eigenvalues(self):
"""
Test that the eigenvalues are correct against numpy's built-in function
"""
np.random.seed(0)
a = np.random.random((20, 20))
a = a @ a.T # make sure it's symmetric
model = QREigendecomposition()
eigenvalues, _ = model.find_eigensystem(a)
self.assertTrue(np.allclose(eigenvalues, np.linalg.eigh(a)[0]), "Eigenvalues are incorrect")
def test_eigenvectors(self):
"""
Test that the eigenvectors are correct against numpy's built-in function
"""
np.random.seed(0)
a = np.random.random((5, 5))
a = a @ a.T # make sure it's symmetric
model = QREigendecomposition()
_, eigenvectors = model.find_eigensystem(a)
## We have to take the absolute value of the eigenvectors because the eigenvectors
## are not unique up to a sign.
self.assertTrue(
np.allclose(np.abs(eigenvectors), np.abs(np.linalg.eigh(a)[1])),
"Eigenvector calculation failed"
)
unittest.main(argv=[''], exit=False)
... ---------------------------------------------------------------------- Ran 3 tests in 0.040s OK
<unittest.main.TestProgram at 0x10f7c04d0>
## Make an interactive video
from ipywidgets import interact, interactive, fixed, interact_manual, Layout
import ipywidgets as widgets
def plotter(i):
amat = model.intermediate[i]
amat /= np.linalg.norm(model.intermediate[i], axis=0, keepdims=True)
plt.figure()
plt.plot([0, amat[:, 0][0]], [0, amat[:, 0][1]])
plt.plot([0, amat[:, 1][0]], [0, amat[:, 1][1]])
plt.show()
interact(
plotter,
i=widgets.IntSlider(0, 0, 10, 1, layout=Layout(width='800px'))
)
interactive(children=(IntSlider(value=0, description='i', layout=Layout(width='800px'), max=10), Output()), _d…
<function __main__.plotter(i)>
## Show the process of A becoming orthogonal
plt.figure(figsize=(9, 1))
for i, amat in enumerate(model.intermediate[:10]):
vec1, vec2 = amat[:, 0], amat[:, 1]
plt.subplot(1, 10, i+1)
plt.plot([0, vec1[0]], [0, vec1[1]], color='red')
plt.plot([0, vec2[0]], [0, vec2[1]], color='blue')
plt.xlim(-0.1, 1)
plt.ylim(-0.1, 1)
plt.axis('off')
Classical Gram-Schmidt: watch out for conditioning!¶
We will create a nearly-singular matrix by first defining a singular matrix, and then adding a small amount of noise to each column vector.
a = np.random.random(4)
for amp in [1e-8, 1.0]:
aa = np.vstack([
a + amp * np.random.random(4),
a + amp * np.random.random(4),
a + amp * np.random.random(4),
a + amp * np.random.random(4),
]).T
print("Condition number: ", np.linalg.cond(aa))
q, r = qr_factorization(aa)
print("Error: ", np.linalg.norm(q @ r - aa))
print("\n")
Condition number: 701085117.6977656 Error: 9.007508107281488e-08 Condition number: 25.86102260636268 Error: 3.1170388806437315e-15
Idea: we want to start dis-aligning the column vectors as early as possible in the iterative algorithm¶
The moment I find a unit vector basis element, immediately remove it from all the remaining column vectors
Recall the curse of dimensionality: in higher dimensions, the condition number tends to be larger, and so the Gram-Schmidt process can be numerically unstable
Another way to think about this: the Gram-Schmidt process is a series of projections. In traditional Gram-Schmidt in high-dimensions, we subtract from the last vector a bunch of very small terms (because the last vector will likely already be close to orthogonal to the previous vectors)
Modified Gram-Schmidt decomposition¶
Traditional Gram-Schmidt
- pick the first column vector
- normalize it
- pick the second column vector
- project vector 2 onto vector 1, multiply by unit vector 1, and then subtract the resulting vector from vector 1
- normalize vector 2
- pick the third column vector, then project to find its components along unit vector 1 AND unit vector 2, then subtract both
- normalize vector 3
- rinse and repeat, subtracting the projects from all previous vectors from the current one in each step
This approach becomes unstable in high-dimensions, where the number of residual subtractions performed on a given column vector gets large. As a result, the elements of the residual vector can become very small before we apply the re-normalization step, leading to numerical errors.
In Modified Gram-Schmidt, we perform the steps in a different order, which allows us to re-normalize after each subtraction of a pair of vectors.
- pick the first column vector
- normalize it
- pick all remaining column vectors, and project them onto the first column vector. Subtract the projections from all of the remaining column vectors
- pick the second column vector
- normalize it.
- rinse and repeat step 3
Besides the order in which we normalize and sweep, the key difference is the step where we compute projections between previously-determined unit-vectors. In the modified Gram-Schmidt, the projection occurs between the latest $i^{th}$ unit vector and a column vector $j > i$ where the previous $i - 1$ unit vectors have already been subtracted out. As a result, our dot product is less likely to be very small, because all of the $i-1$ previous shared basis vectors have already been removed by the time we compute the dot product.
- As we saw with ill-conditioned matrices, numerical operations usually behave better when the involved vectors are further from parallel. modified GS sidesteps finding the dot product between two nearly-aligned vectors.
class QRFactorizationSolver:
"""
Solver a linear problem using preconditioning with QR factorization. Implements both
the traditional Gram-Schmidt process and the modified Gram-Schmidt process.
"""
def __init__(self, store_history=True):
self.store_history = store_history
if self.store_history:
self.history = []
def qr0(self, X):
"""
Perform QR factorization using classical Gram-Schmidt process.
"""
self.Q = np.copy(X) # Orthonormal vectors will be stored here
self.R = np.zeros_like(X, dtype=float)
## Store the initial guess
if self.store_history:
self.history.append(self.Q.copy())
# Loop over column vectors
for i in range(X.shape[1]):
# pick out the i-th column vector as the pivot
v = np.copy(X[:, i])
# Sweep over all previous Q-vectors and subtract off the projections
# This can be vectorized, but we'll do it in a loop for clarity
for j in range(i):
self.R[j, i] = np.dot(self.Q[:, j], X[:, i])
v -= self.R[j, i] * self.Q[:, j]
self.R[i, i] = np.linalg.norm(v)
self.Q[:, i] = v / self.R[i, i]
if self.store_history:
self.history.append(self.Q.copy())
return self.Q, self.R
# Loop over column vectors
def qr(self, X):
self.Q = np.copy(X) # initial guess is just the original basis
self.R = np.zeros_like(X, dtype=float)
## Store the initial guess
if self.store_history:
self.history.append(self.Q.copy())
for i in range(X.shape[1]):
# Calculate diagonal element of R before normalizing Q
self.R[i, i] = np.linalg.norm(self.Q[:, i])
# Normalize the i-th column of Q
self.Q[:, i] /= self.R[i, i]
# Loop to update remaining columns by removing the i-th column component
# along each of the previous columns
for j in range(i + 1, X.shape[1]):
self.R[i, j] = np.dot(self.Q[:, i], self.Q[:, j])
self.Q[:, j] -= self.R[i, j] * self.Q[:, i]
if self.store_history:
self.history.append(self.Q.copy())
return self.Q, self.R
def solve(self, A, b):
"""
Solve Ax = b using QR factorization. We can see the
factorization as a form of preconditioning for the linear solver
"""
Q = self.qr(A)[0]
y = np.dot(Q.T, b)
return np.linalg.solve(self.R, y) # O(N^2) solve because R is upper triangular
def test_qr(self):
"""
Test the QR factorization solver
"""
a = np.random.randn(3, 3)
q, r = self.qr(a)
assert np.allclose(a, q @ r)
def test_solver(self):
A = np.random.randn(5, 5)
b = np.random.randn(5)
x = self.solve(A, b)
assert np.allclose(np.dot(A, x), b)
a = np.random.random((5, 5))
model = QRFactorizationSolver()
plt.figure()
plt.subplot(1, 2, 1)
plt.imshow(
model.qr0(a)[0]
)
plt.title('Traditional Gram-Schmidt: Q')
plt.subplot(1, 2, 2)
plt.imshow(
model.qr(a)[0]
)
plt.title('Modified Gram-Schmidt: Q')
plt.figure()
plt.figure()
plt.subplot(1, 2, 1)
plt.imshow(
model.qr0(a)[1]
)
plt.title('Traditional Gram-Schmidt: R')
plt.subplot(1, 2, 2)
plt.imshow(
model.qr(a)[1]
)
plt.title('Modified Gram-Schmidt: R')
print(np.allclose(model.qr0(a)[0], model.qr(a)[0]))
True
<Figure size 640x480 with 0 Axes>
We can visualize the difference between Gram-Schmidt and Modified Gram-Schmidt by inspecting how the columnspace changes at each iteration of the algorithm
np.random.seed(0)
A = np.random.random((100, 100))
model = QRFactorizationSolver(store_history=True)
model.qr0(A.copy())
qr_trad = np.array(model.history).copy()
model = QRFactorizationSolver(store_history=True)
model.qr(A.copy())
qr_mod = np.array(model.history).copy()
## Make an interactive video
from ipywidgets import interact, interactive, fixed, interact_manual, Layout
import ipywidgets as widgets
def plotter(i):
amat = qr_trad[i]
amat /= np.linalg.norm(amat, axis=0, keepdims=True)
plt.figure()
plt.plot([0, amat[:, 0][0]], [0, amat[:, 0][1]])
plt.plot([0, amat[:, 10][0]], [0, amat[:, 20][1]])
plt.plot([0, amat[:, 10][0]], [0, amat[:, 40][1]])
plt.plot([0, amat[:, 50][0]], [0, amat[:, 60][1]])
plt.plot([0, amat[:, 99][0]], [0, amat[:, 99][1]])
plt.text(0.1, 0.1, str(i), fontsize=20)
plt.xlim([-0.15, 0.15])
plt.ylim([-0.15, 0.15])
plt.show()
interact(
plotter,
i=widgets.IntSlider(0, 0, len(qr_trad) - 1, 1, layout=Layout(width='800px'))
)
def plotter(i):
amat = qr_mod[i]
amat /= np.linalg.norm(amat, axis=0, keepdims=True)
plt.figure()
plt.plot([0, amat[:, 0][0]], [0, amat[:, 0][1]])
plt.plot([0, amat[:, 10][0]], [0, amat[:, 20][1]])
plt.plot([0, amat[:, 10][0]], [0, amat[:, 40][1]])
plt.plot([0, amat[:, 50][0]], [0, amat[:, 60][1]])
plt.plot([0, amat[:, 99][0]], [0, amat[:, 99][1]])
## label current pivot index of the QR factorization overlaid on graph as text
plt.text(0.1, 0.1, str(i), fontsize=20)
plt.xlim([-0.15, 0.15])
plt.ylim([-0.15, 0.15])
plt.show()
interact(
plotter,
i=widgets.IntSlider(0, 0, len(qr_trad) - 1, 1, layout=Layout(width='800px'))
)
interactive(children=(IntSlider(value=0, description='i', layout=Layout(width='800px')), Output()), _dom_class…
interactive(children=(IntSlider(value=0, description='i', layout=Layout(width='800px')), Output()), _dom_class…
<function __main__.plotter(i)>
## plot still frames
plt.figure(figsize=(10, 10))
for i in range(0, len(qr_trad)-1, 1):
plt.subplot(10, 10, i+1)
amat = qr_trad[i]
amat /= np.linalg.norm(amat, axis=0, keepdims=True)
plt.plot([0, amat[:, 0][0]], [0, amat[:, 0][1]])
plt.plot([0, amat[:, 10][0]], [0, amat[:, 20][1]])
plt.plot([0, amat[:, 10][0]], [0, amat[:, 40][1]])
plt.plot([0, amat[:, 50][0]], [0, amat[:, 60][1]])
plt.plot([0, amat[:, 99][0]], [0, amat[:, 99][1]])
plt.xlim([-0.15, 0.15])
plt.ylim([-0.15, 0.15])
plt.axis('off')
## plot still frames
plt.figure(figsize=(10, 10))
for i in range(0, len(qr_mod)-1, 1):
plt.subplot(10, 10, i+1)
amat = qr_mod[i]
amat /= np.linalg.norm(amat, axis=0, keepdims=True)
plt.plot([0, amat[:, 0][0]], [0, amat[:, 0][1]])
plt.plot([0, amat[:, 10][0]], [0, amat[:, 20][1]])
plt.plot([0, amat[:, 10][0]], [0, amat[:, 40][1]])
plt.plot([0, amat[:, 50][0]], [0, amat[:, 60][1]])
plt.plot([0, amat[:, 99][0]], [0, amat[:, 99][1]])
plt.xlim([-0.15, 0.15])
plt.ylim([-0.15, 0.15])
plt.axis('off')
We can now check the condition number of the matrix, and see how it affects the error of the QR decomposition.
a = np.random.random(1000)
amp = 0.1
for amp in [1e-16, 1.0]:
print("Amplitude: ", amp)
## Build an ill-conditioned matrix by repeating the bearing vector a and adding noise
aa = np.tile(a, (len(a), 1)).T + np.random.random(size=(len(a), len(a))) * amp
print("Condition number: ", np.linalg.cond(aa))
model = QRFactorizationSolver()
q, r = model.qr0(aa)
# q, r = qr_factorization(aa)
print("Traditional Error: ", np.linalg.norm(q @ r - aa))
q, r = model.qr(aa)
# q, r = qr_factorization(aa)
print("Modified Error: ", np.linalg.norm(q @ r - aa))
print("\n")
Amplitude: 1e-16 Condition number: 2.4747871550088856e+20 Traditional Error: 8.954280768711371e-11 Modified Error: 5.818319059624814e-14 Amplitude: 1.0 Condition number: 88233.24942194215 Traditional Error: 1.0122218953707907e-12 Modified Error: 1.0136737919797968e-12
Because we stored all the intermediate values of the QR factorization, we can create a time series how the condition number of the intermediate matrices $A_k$ changes as we perform the QR algorithm
all_cond_trad = list()
all_cond_mod = list()
for i in range(0, len(qr_trad)):
all_cond_trad.append(np.linalg.cond(qr_trad[i]))
all_cond_mod.append(np.linalg.cond(qr_mod[i]))
plt.figure(figsize=(8, 5))
plt.plot(all_cond_trad, label='Traditional')
plt.plot(all_cond_mod, label='Modified')
plt.legend()
plt.title('Condition number of Q matrix during QR factorization')
plt.xlabel('Iteration')
plt.ylabel('Condition number')
Text(0, 0.5, 'Condition number')
Text(0, 0.5, 'Condition number')
Community detection on the co-authorship network of physicists¶
- We revisit the network consisting of coauthorship among physicists based arXiv postings in
astro-ph - The graph contains $N = 18772$ nodes, which correspond to unique authors observed over the period 1993 -- 2003
- If Author i and Author j coauthored a paper during that period, the nodes are connected
- In order to analyze this large graph, we will downsample it to a smaller graph with $N = 1000$ nodes representing the most highly-connected authors
- This dataset is from the Stanford SNAP database
import networkx as nx
## Load the full coauthorship network
fpath = "../resources/ca-AstroPh.txt.gz"
# fpath = "../resources/ca-CondMat.txt.gz"
g = nx.read_edgelist(fpath)
## Create a subgraph of the 1000 most connected authors
subgraph = sorted(g.degree, key=lambda x: x[1], reverse=True)[:4000]
subgraph = [x[0] for x in subgraph]
g2 = g.subgraph(subgraph)
# rename nodes to sequential integers as they would appear in an adjacency matrix
g2 = nx.convert_node_labels_to_integers(g2, first_label=0)
pos = nx.spring_layout(g2)
# pos = nx.kamada_kawai_layout(g2)
# nx.draw_spring(g2, pos=pos, node_size=10, node_color='black', edge_color='gray', width=0.5)
nx.draw(g2, pos=pos, node_size=5, node_color='black', edge_color='gray', width=0.5, alpha=0.5)
plt.show()
Random walks on graph: The ensemble limit¶
Recall that random walks on this graph exhibited a non-uniform invariant distribution, where the probability of visiting a node was proportional to its degree.
This is because we can interpret the adjacency matrix $A$ as a transition matrix for a Markov chain, which governs the dynamics of an ensemble of random walkers on the graph. The probability of transitioning from node $i$ to node $j$ in one step is given by the transition matrix $P_{ij} = A_{ij} / \sum_k A_{ik}$, where the denominator is the out-degree of node $i$. Notice that even if $A$ is symmetric, $P$ is not symmetric, because the transition probability depends on the out-degree of the node.
What is the long-term behavior of this Markov chain? We can find the invariant distribution $\pi$ by solving the equation $\pi = \pi P$, which is equivalent to finding the eigenvector of $P$ with eigenvalue 1.
Our definition of the Markov chain implies that we are treating the adjacency matrix as defining a Markov chain in discrete time
Spectral graph analysis¶
We can see that there is a clump of highly-collaborative authors, and then isolated subcommunities. We can quantify this observation and these clumps using spectral analysis of the graph
We define the adjacency matrix $A$ of the graph as a matrix where $A_{ij} = 1$ if nodes $i$ and $j$ are connected, and $A_{ij} = 0$ otherwise. We define a Markov transition matrix from this adjacency matrix as
$$ T_{ij} = \frac{A_{ij}}{\sum_k A_{ik}} $$
where the denominator is the total number of connections for node $i$. This matrix is row-stochastic, meaning that the sum of each row is 1. This matrix represents a random walk on the graph, where at each step, we randomly select a neighbor of the current node, and then move to that node. The probability of moving to a given node is proportional to the number of connections that node has to the current node.
# use spectral graph partitioning
## Create the adjacency matrix
A = nx.adjacency_matrix(g2).todense()
A = np.array(A)
# convert to discrete-time Markov transition matrix
T = A / np.sum(A, axis=0, keepdims=True)
## Create the degree matrix
# D = np.diag(np.sum(A, axis=0))
# D = np.identity(A.shape[0]) # unweighted graph
## Create the graph Laplacian matrix
# L = D - A
## Compute the eigenvalues and eigenvectors
eigenvalues, eigenvectors = np.linalg.eig(T)
## Sort the eigenvalues and eigenvectors
sort_inds = np.argsort(eigenvalues)[::-1]
eigenvalues, eigenvectors = eigenvalues[sort_inds], eigenvectors[:, sort_inds]
## Plot the eigenvalues in descending order
plt.figure(figsize=(8, 5))
plt.plot(eigenvalues)
plt.title("Eigenvalues of the Transition matrix")
## Plot the leading eigenvectors as colors on the graph
plt.figure(figsize=(12, 12))
for i in range(9):
plt.subplot(3, 3, i+1)
nx.draw(g2, pos=pos, node_size=200, node_color=np.log(np.abs(eigenvectors[:, i])), edge_color='gray', width=0.5, alpha=0.5)
plt.title("Eigenvector {}".format(i+1))
/Users/william/micromamba/envs/cphy/lib/python3.11/site-packages/matplotlib/cbook.py:1699: ComplexWarning: Casting complex values to real discards the imaginary part return math.isfinite(val) /Users/william/micromamba/envs/cphy/lib/python3.11/site-packages/matplotlib/cbook.py:1345: ComplexWarning: Casting complex values to real discards the imaginary part return np.asarray(x, float)
What do the different eigenvectors mean?¶
Leading Eigenvalues¶
A discrete-time Markov chain has leading eigenvector associated with the eigenvalue 1. This eigenvector represents the invariant distribution of the Markov chain, and is the long-term probability of finding the random walker at a given node.
- If there are multiple disconnected subgraphs, there will be degeneracy with multiple eigenvectors associated with the eigenvalue 1.
The second eigenvector of the transition matrix is associated with the second-largest eigenvalue. This represents the longest-lived transients in the Markov chain dynamics
Negative Eigenvalue¶
- If there are negative eigenvalues, these indicate cycles in the graph. The eigenvectors associated with these eigenvalues represent the oscillatory behavior of the random walker as it cycles through the graph. For example, consider the transition matrix:
$$ A = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} $$
A random walker will oscillate between the two nodes. The invariant density associated with the leading eigenvalue $\lambda_1 = 1$ is given by
$$ \pi_1 = \frac{1}{2} \begin{bmatrix} 1 \\ 1 \end{bmatrix} $$
Because, on average, the walker spends half of its time at each node. The eigenvector associated with the second eigenvalue $\lambda_2 = -1$ is given by
$$ \begin{bmatrix} 1 \\ -1 \end{bmatrix} $$
Because the walker spends one step at the first node, and then one step at the second node, and then repeats this cycle.
Laplacian eigenmaps¶
We saw that we can associate a discrete-time Markov chain with the adjacency matrix $A$ of a graph. We can also associate a continuous-time Markov chain with the adjacency matrix of a graph. In this case, the generator matrix is defined as
$$ Q_{ij} = \begin{cases} A_{ij} & i \neq j \\ - \sum_k A_{ik} & i = j \end{cases} $$
This defines a continuous-time Markov chain, with differential equation
$$ \frac{d}{dt} \pi(t) = Q \pi(t) $$
where $\pi(t)$ is the probability distribution of the random walker at time $t$. The solution to this differential equation is given by $$ \pi(t) = e^{Qt} \pi(0) $$ where $e^{Qt}$ is the matrix exponential.
The generator matrix $Q$ is related to the transition matrix $P$ by the relation $Q = P - \mathbb{I}$, where $\mathbb{I}$ is the identity matrix. This means that the eigenvalues of $Q$ are related to the eigenvalues of $P$ by $\lambda_Q = \lambda_P - 1$. This means that the leading eigenvalue of $Q$ is 0, and the leading eigenvector of $Q$ is the same as the leading eigenvector of $P$.
The Graph Laplacian¶
The graph Laplacian is defined as
$$ L = D - A $$
where $D$ is a diagonal matrix, where $D_{ii}$ is the degree of node $i$. The graph Laplacian is a symmetric matrix, and so it has a complete set of orthonormal eigenvectors. The eigenvectors of the graph Laplacian are related to the eigenvectors of the transition matrix $P$ by
$$ \phi_i = \frac{1}{\sqrt{d_i}} \psi_i $$
where $d_i$ is the degree of node $i$.
import networkx as nx
from scipy.sparse.linalg import eigs
from scipy.sparse import csr_matrix
class LaplacianEigenmap:
"""
A class for computing the Laplacian Eigenmap of a graph
Attributes:
n_components (int): The number of components to return.
"""
def __init__(self, n_components=2):
self.n_components = n_components
def amat_to_dist(self, A):
"""convert adjacency matrix to distance matrix with shortest path"""
g2 = nx.DiGraph(np.array(A))
A = csr_matrix(A)
dist = np.zeros(A.shape)
for i in range(A.shape[0]):
for j in range(A.shape[1]):
try:
dist[i, j] = nx.shortest_path_length(g2, i, j)
except:
dist[i, j] = 1e10
return dist
def fit_transform(self, A):
# A is the adjacency matrix
# Convert adjacency matrix to distance matrix
A = self.amat_to_dist(A)
# Compute degree matrix
D = np.diag(np.sum(A, axis=1)).astype(float)
# Compute Laplacian matrix
L = (D - A).astype(float)
# Eigendecomposition
vals, vecs = eigs(csr_matrix(L, dtype='float64'), k=self.n_components + 1,
M=csr_matrix(D, dtype='float64'), which='SM')
# Sort eigenpairs and get relevant eigenvectors
sorted_indices = np.argsort(vals.real)
relevant_indices = sorted_indices[1:self.n_components + 1] # Exclude smallest eigenvalue
# Projected data
Y = vecs[:, relevant_indices].real
return Y
model = LaplacianEigenmap(n_components=2)
Y = model.fit_transform(A[:500, :500])
plt.figure(figsize=(8, 8))
plt.scatter(Y[:, 0], Y[:, 1], s=4, c='black')
plt.title("Laplacian Eigenmap")
Text(0.5, 1.0, 'Laplacian Eigenmap')
Y.shape
(100, 2)
How do we interpret the eigenspectrum of a graph?¶
The eigenvecors of the adjacency matrix of a graph represent the "modes" of the graph
The graph adjacency matrix can be used to define a Markov process on the graph, which evolves a probability distribution of random walkers over the nodes of the graph.
The leading eigenvector of the adjacency matrix represents the stationary distributions of this Markov process, while the subsequent eigenvectors represent long-lived transients
The first eigenvector thus gives the long-term probability distribution of which nodes random walkers will be found on, and so it can be used as a loose ranking of the importance of nodes in the graph
How do we visualize graphs?¶
class MultidimensionalScaling:
def __init__(self, A):
self.A = A
def adj_to_dist(self, A):
"""
Convert an unweighted adjacency matrix to a distance matrix using the
shortest path distance between nodes.
"""
# dijkstra's algorithm
dist = np.zeros_like(A, dtype=float)
for i in range(A.shape[0]):
for j in range(A.shape[1]):
if i == j:
continue
if A[i, j] == 0:
dist[i, j] = np.inf
else:
dist[i, j] = 1
for k in range(A.shape[0]):
for i in range(A.shape[0]):
for j in range(A.shape[0]):
dist[i, j] = min(dist[i, j], dist[i, k] + dist[k, j])
return dist
def fit_transform(self, n_components=2):
"""
Fit the MDS model to the data
Args:
n_components (int): The number of dimensions to project into.
Returns:
X (numpy.ndarray): The projected data.
"""
n = self.A.shape[0]
dim = n_components
dmat = self.adj_to_dist(self.A)
# Step 1: Create the centering matrix
H = np.eye(n) - np.ones((n, n)) / n
# Step 2: Apply double centering
B = -0.5 * np.dot(H, np.dot(dmat ** 2, H))
# Step 3: Eigen decomposition
eigenvalues, eigenvectors = np.linalg.eigh(B)
# Step 4: Sort and select top k eigenvalues and eigenvectors
sorted_idx = np.argsort(eigenvalues)[::-1]
lambda_sqrt = np.sqrt(np.diag(eigenvalues[sorted_idx][:dim]))
E = eigenvectors[:, sorted_idx][:, :dim]
# Step 5: Compute coordinates
X = np.dot(E, lambda_sqrt)
return X
model = MultidimensionalScaling(A)
X_pos = model.fit_transform(n_components=2)
plt.figure(figsize=(12, 12))
plt.plot(X_pos[:, 0], X_pos[:, 1], '.')
--------------------------------------------------------------------------- KeyboardInterrupt Traceback (most recent call last) Cell In[168], line 62 59 return X 61 model = MultidimensionalScaling(A) ---> 62 X_pos = model.fit_transform(n_components=2) 64 plt.figure(figsize=(12, 12)) 65 plt.plot(X_pos[:, 0], X_pos[:, 1], '.') Cell In[168], line 40, in MultidimensionalScaling.fit_transform(self, n_components) 37 n = self.A.shape[0] 38 dim = n_components ---> 40 dmat = self.adj_to_dist(self.A) 42 # Step 1: Create the centering matrix 43 H = np.eye(n) - np.ones((n, n)) / n Cell In[168], line 24, in MultidimensionalScaling.adj_to_dist(self, A) 22 for i in range(A.shape[0]): 23 for j in range(A.shape[0]): ---> 24 dist[i, j] = min(dist[i, j], dist[i, k] + dist[k, j]) 25 return dist KeyboardInterrupt: