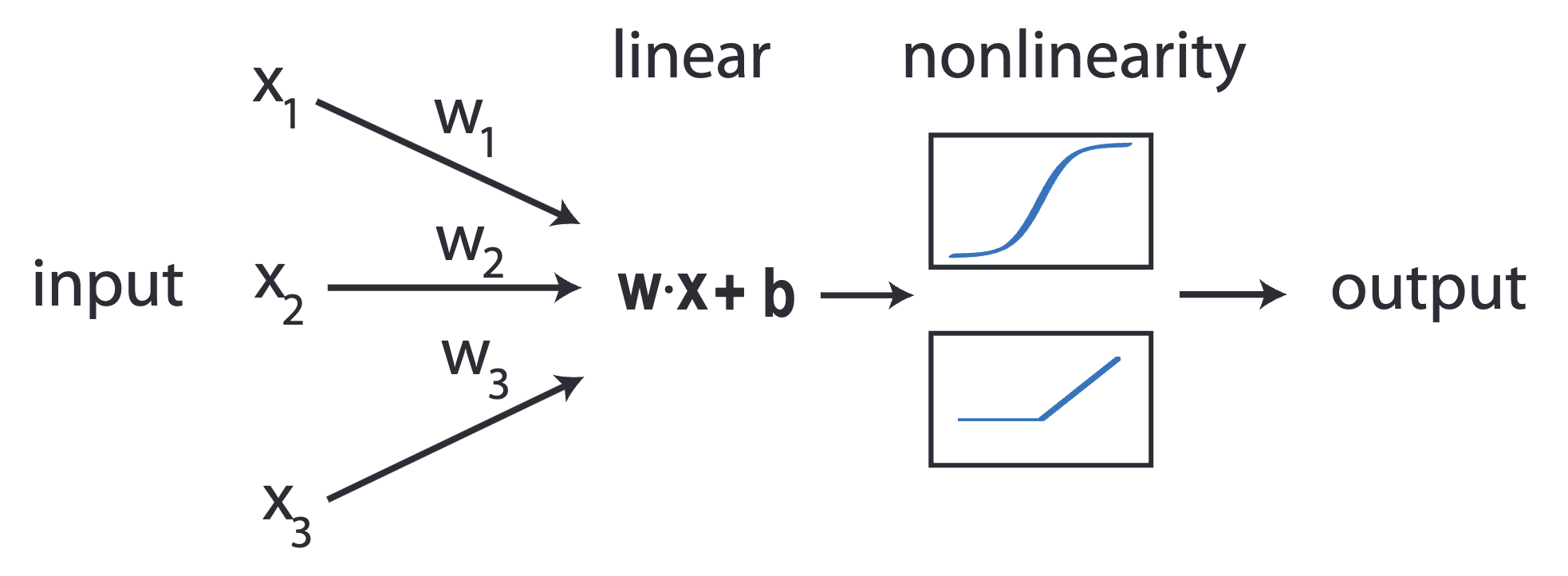
Deep neural networks and decision boundaries¶

Preamble: Run the cells below to import the necessary Python packages

This notebook created by William Gilpin. Consult the course website for all content and GitHub repository for raw files and runnable online code.

In [4]:
## Preamble / required packages
import numpy as np
np.random.seed(0)

## Import local plotting functions and in-notebook displazooy functions
import matplotlib.pyplot as plt
from IPython.display import Image, display
%matplotlib inline

import warnings
## Comment this out to activate warnings
warnings.filterwarnings('ignore')

Is there anything linear models can't do?¶

  • We previously saw that regularized linear models can be surprisingly effective for supervised learning tasks like forecasting, regression, and even classification.

  • In unsupervised learning, PCA and its variants can be thought of as linear models

  • Are there any problems that are fundamentally beyond the capabilities of linear models?

In [3]:
## AND dataset for training
X = np.array([[0.0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 0, 0.0, 1.0])

print("Training data has shape: ", X.shape)
print("Target targets have shape: ", y.shape)

## Plot the AND dataset
plt.figure(figsize=(5, 5))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=500)
plt.xlabel("X Feature 1")
plt.ylabel("X Feature 2")
plt.colorbar(label="Target")

Training data has shape:  (4, 2)
Target targets have shape:  (4,)
Out[3]:
<matplotlib.colorbar.Colorbar at 0x1179ac2d0>
No description has been provided for this image

  • Since there are discrete-valued labels for each data point, we can think of this as a classification problem.

  • We will now fit a logistic regression model to this data, and then visualize the predicted test labels

In [5]:
## train logistic regression model
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(penalty='none')
model.fit(X, y)
yhat = model.predict(X)

print("Predicted labels have shape: ", yhat.shape)
print("Train accuracy: ", np.mean(yhat == y))

plt.figure(figsize=(5, 5))
plt.scatter(X[:, 0], X[:, 1], c=yhat, cmap=plt.cm.coolwarm, s=500)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")

print(yhat)

Predicted labels have shape:  (4,)
Train accuracy:  1.0
[0. 0. 0. 1.]
No description has been provided for this image

Decision boundaries¶

  • In the above plot, we visualized the predicted labels specifically for the training datapoints

  • However, in principle the training features can have any values in the feature space, and so we can construct a testing dataset spanning the domain of the feature space.

  • For a trained classification model, labelling each point in this domain reveals the decision boundary of the model

In [6]:
## plot decision boundary
def plot_decision_boundary(X, y, clf):
    """
    Plot the decision boundary of a trained classifier clf

    Args:
        X (numpy.ndarray): Input data
        y (numpy.ndarray): Input labels
        clf (sklearn.base.BaseEstimator): Trained classifier

    Returns:
        None
    """
    # Set min and max values and give it some padding
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01

    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    # Predict the function value for the whole gid
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])

    # Put the result into a color plot
    Z = Z.reshape(xx.shape)
    
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap='bwr')
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap='bwr')

plt.figure(figsize=(5, 5))
plot_decision_boundary(X, y, model)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Decision boundary for Logistic classifier on AND dataset")
Out[6]:
Text(0.5, 1.0, 'Decision boundary for Logistic classifier on AND dataset')
No description has been provided for this image

Questions¶

  • Why is the decision boundary a straight line?

  • What might influence the location and slope of the decision boundary?

Another simple dataset¶

In [8]:
## XOR dataset for training
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 1.0, 1.0, 0.0])

## Plot the XOR dataset
plt.figure(figsize=(5, 5))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=500)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")


print(X.shape) 
print(y.shape)

(4, 2)
(4,)
No description has been provided for this image
In [9]:
## train logistic regression model
from sklearn.linear_model import LogisticRegression

## XOR dataset for training
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 1.0, 1.0, 0.0])

model = LogisticRegression(penalty='none')
model.fit(X, y)
yhat = model.predict(X)

print("Predicted labels have shape: ", yhat.shape)
print("Train accuracy: ", np.mean(yhat == y))

Predicted labels have shape:  (4,)
Train accuracy:  0.5
In [10]:
# plt.figure()
# plt.scatter(X[:, 0], X[:, 1], c=yhat, cmap=plt.cm.coolwarm, s=500)
# plt.xlabel("Feature 1")
# plt.ylabel("Feature 2")


plt.figure(figsize=(5, 5))
plot_decision_boundary(X, y, model)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Decision boundary for Logistic classifier on XOR dataset")
Out[10]:
Text(0.5, 1.0, 'Decision boundary for Logistic classifier on XOR dataset')
No description has been provided for this image

What is a neural network?¶

  • A neural network is a function that takes a vector of inputs and returns a vector of outputs
  • Anything for which you can use a matrix, you can use a neural network
  • Like linear regression, the entries in the matrix are trainable parameters

Linear regression¶

$$ \hat{y} = \boldsymbol{\theta} X $$

Generalized linear regression¶

$$ \hat{y} = \sigma(\boldsymbol{\theta} X) $$ where $\sigma(\cdot)$ is a nonlinear "link" function. For logistic function, $\sigma(u) = {1}/({1 + e^{-u}})$

Multilayer perceptron (a neural network)¶

$$ \hat{y} = \sigma(\boldsymbol{\theta}_2 \sigma(\boldsymbol{\theta}_1 X)) $$

where $\sigma$ is a nonlinear function, and $\boldsymbol{\theta}$ is a matrix of trainable parameters.

In [22]:
## TODO: Add noise to inputs

from sklearn.neural_network import MLPClassifier

model = MLPClassifier(hidden_layer_sizes=(5, 300, 300, 5), activation='tanh', max_iter=1000, random_state=0)

## XOR dataset for training
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 1.0, 1.0, 0.0])

## AND
# X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
# y = np.array([0, 0.0, 0.0, 1.0])

model.fit(X, y)
yhat = model.predict(X)

plt.figure(figsize=(5, 5))
plt.scatter(X[:, 0], X[:, 1], c=yhat, cmap=plt.cm.coolwarm, s=500)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")

plt.figure(figsize=(5, 5))
plot_decision_boundary(X, yhat, model)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
Out[22]:
Text(0, 0.5, 'Feature 2')
No description has been provided for this image
No description has been provided for this image
In [ ]:
## Read out the weight matrices
# model.coefs_

for layer in model.coefs_:
    print(layer.shape)

(2, 5)
(5, 5)
(5, 1)
In [ ]:

What do neural networks do?¶

  • Neural networks can learn "arbitrary" nonlinear functions of the data
  • Cybenko's theorem: any continuous function can be approximated by a neural network with a single, sufficiently wide hidden layer
    • Modern generalizations exist for deep networks, etc

Multilayer perceptron¶

  • Simplest neural network: multilayer perceptron: matrix multiplication followed by a nonlinear function

  • Hyperparameters: depth is number of layers, width is number of "neurons" (units) per layer, activation function, regularization, etc

  • The number of trainable parameters is the number of entries across all matrices. Overparameterized in many cases.

In [60]:
Image('../resources/mlp.png')
# https://medium.com/codex/introduction-to-how-an-multilayer-perceptron-works-but-without-complicated-math-a423979897ac
Out[60]:
No description has been provided for this image

The diagram above is equivalent to writing

$$ \hat{\mathbf{y}} = \sigma(\boldsymbol{\theta}_3\sigma(\boldsymbol{\theta}_2 \sigma(\boldsymbol{\theta}_1 X))) $$

where $\boldsymbol{\theta}_1 \in \mathbb{R}^{5 \times 5}$, $\boldsymbol{\theta}_2 \in \mathbb{R}^{5 \times 5}$, $\boldsymbol{\theta}_3 \in \mathbb{R}^{5 \times 2}$

In [14]:
## The code version

def mlp_forward(X):
    theta1 = np.random.random((5, 5))
    theta2 = np.random.random((5, 5))
    theta3 = np.random.random((5, 2))

    h1 = np.tanh(X @ theta1)
    h2 = np.tanh(h1 @ theta2)
    h3 = np.tanh(h2 @ theta3)

    return h3


X = np.random.random((10000, 5))

print("Input shape: ", X.shape)
print("Output shape: ", mlp_forward(X).shape)

Input shape:  (10000, 5)
Output shape:  (10000, 2)

The choice of activation function is itself a hyperparameter¶

In [45]:
import numpy as np
import matplotlib.pyplot as plt

# Define the activation functions
def hopfield(z):
    return np.where(z >= 0, 1, 0)

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def tanh(z):
    return np.tanh(z)

def relu(z):
    return np.maximum(0, z)

def leaky_relu(z, alpha=0.1):
    return np.where(z > 0, z, alpha * z)

def elu(z, alpha=1.0):
    return np.where(z > 0, z, alpha * (np.exp(z) - 1))

def selu(z, lambda_=1.0507, alpha=1.67326):
    return np.where(z > 0, lambda_ * z, lambda_ * alpha * (np.exp(z) - 1))

def silu(z):
    return z / (1 + np.exp(-z))

def softplus(z):
    return np.log(1 + np.exp(z))

# Set up the figure and axis
z = np.linspace(-5, 5, 100)
fig, axs = plt.subplots(3, 3, figsize=(12, 9), facecolor='black')
# fig.subplots_adjust(hspace=0.5, wspace=0.4)
fig.subplots_adjust(hspace=0.6, wspace=0.4, top=0.92, bottom=0.08)


# Define titles and functions for each subplot
titles = [
    'Hopfield', 'Sigmoid', 'Tanh', 'ReLU', 'Leaky ReLU', 'ELU',
    'SELU', 'SiLU', 'Softplus'
]
functions = [
    hopfield, sigmoid, tanh, relu, leaky_relu, elu,
    selu, silu, softplus
]
equations = [
    r"$\Theta(z)$",
    r"$\frac{1}{1+e^{-z}}$",
    r"$\tanh(z)$",
    r"$\max(0, z)$",
    r"$0.1z$ if $z \leq 0$, $z$ if $z > 0$",
    r"$e^z - 1$ if $z \leq 0$, $z$ if $z > 0$",
    r"$\lambda z$ if $z > 0$, $\lambda \alpha (e^z - 1)$ if $z \leq 0$",
    r"$z \cdot \sigma(z)$ where $\sigma(z) = \frac{1}{1 + e^{-z}}$",
    r"$\log(1 + e^z)$"
]

# Plot each activation function
for i, (ax, title, func, equation) in enumerate(zip(axs.flat, titles, functions, equations)):
    ax.plot(z, func(z), color='orange', linewidth=2)
    ax.set_title(title, fontsize=16, color='white')
    ax.text(0, -0.5, equation, fontsize=12, color='white', ha='center')
    ax.grid(False)
    ax.set_facecolor('black')
    ax.spines['bottom'].set_color('white')
    ax.spines['left'].set_color('white')
    ax.tick_params(axis='x', colors='white')
    ax.tick_params(axis='y', colors='white')
    if i < 3:
        ax.set_ylim(-1, 1.1)
    elif i < 6:
        ax.set_ylim(-1, 6)
    else:
        ax.set_ylim(-1.8, 6)

plt.show()
No description has been provided for this image
In [ ]:

A harder classification problem: predicting the Reynolds number of turbulent flows¶

  • We will use a dataset of videos of 2D turbulent flows simulated at different Reynolds numbers

  • This dataset has spatial noise, which is a common artifact of the PIV algorithm used to extract a velocity field from videos of a flow

  • Each frame we will treat as a single datapoint in our dataset, with a number of features equal to the number of pixels in the frame

  • We will focus on the far-field wake of a cylinder, rather than the near-field, since this is a harder problem that is less obvious to the naked eye

In [5]:
## load the turbulence dataset

all_vorticity_fields = list()
all_reynolds_numbers = list()

# Load simulations for different Reynolds numbers
re_vals = [300, 600, 900, 1200]
for re_val in re_vals:

    # Load the two-dimensional velocity field data. Data is stored in a 4D numpy array,
    # where the first dimension is the time index, the second and third dimensions are the
    # x and y coordinates, and the fourth dimension is the velocity components (ux or uv).
    vfield = np.load(
        f"../resources/von_karman_street/vortex_street_velocities_Re_{re_val}_largefile.npz", 
        allow_pickle=True
    )

    # Calculate the vorticity, which is the curl of the velocity field
    vort_field = np.diff(vfield, axis=1)[..., :-1, 1] + np.diff(vfield, axis=2)[:, :-1, :, 0]

    # Downsample the dataset
    vort_field = vort_field[::6, -127:, :]

    # Add random experimental noise
    noise_field = np.random.normal(0, 0.02, vort_field.shape)
    ## Gaussian blur the noise field along the x and y axes using scipy.ndimage.gaussian_filter
    from scipy.ndimage import gaussian_filter
    noise_field = gaussian_filter(noise_field, sigma=(0, 4, 4))

    vort_field += noise_field


    all_vorticity_fields.append(vort_field)
    all_reynolds_numbers.extend(re_val * np.ones(vort_field.shape[0]))

all_vorticity_fields = np.vstack(all_vorticity_fields)
all_reynolds_numbers = np.array(all_reynolds_numbers)

print("Vorticity field data has shape: {}".format(all_vorticity_fields.shape))
print("Reynolds number data has shape: {}".format(all_reynolds_numbers.shape))


## Plot 4x4 grid of vorticity fields
fig, ax = plt.subplots(4, 4, figsize=(8, 8))
for i in range(4):
    re_val = re_vals[i]
    for j in range(4):
        ax[j, i].imshow(
            all_vorticity_fields[all_reynolds_numbers == re_val][150 * j], 
            cmap='bwr',
            vmin=-0.01, vmax=0.01
        )
        ax[j, i].axis('off')
        if j == 0:
            ax[j, i].set_title(f"Re = {re_val}")
plt.tight_layout()
fig.subplots_adjust(wspace=0.1, hspace=0.1)

Vorticity field data has shape: (2000, 127, 127)
Reynolds number data has shape: (2000,)
No description has been provided for this image
In [ ]:

Flattening¶

Our images have resolution 127x127, so we have 16129 features per frame. We will use a dataset of 1000 frames, and we will need to flatten each frame into a vector of length 16129.

In [32]:
## Convert into a machine-learning dataset by flattening features

# Flatten the vorticity field data
X = np.reshape(all_vorticity_fields, (all_vorticity_fields.shape[0], -1))
# Standardize the data
X = (X - np.mean(X, axis=0)) / np.std(X, axis=0)
y = all_reynolds_numbers

print("Training data has shape: {}".format(X.shape))
print("Training labels have shape: {}".format(y.shape))

Training data has shape: (2000, 16129)
Training labels have shape: (2000,)

How hard is this problem? Try playing with unsupervised embeddings to evaluate the difficulty¶

  • Before we train a supervised model, let's try to visualize the data using some unsupervised learning techniques

  • Unsupervised techniques can tell us how hard the problem is, and what kind of structure the data has

  • Question: Why are these lines?

In [7]:
from sklearn.decomposition import PCA

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

plt.figure(figsize=(9, 8))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=all_reynolds_numbers)
plt.xlabel("PCA component 1")
plt.ylabel("PCA component 2")
plt.colorbar(label="Reynolds number")
Out[7]:
<matplotlib.colorbar.Colorbar at 0x339e0c950>
No description has been provided for this image

We can also try to visualize the data using a nonlinear embedding technique like UMAP. This method generally does not preserve distances (isometry), but the nearest neighbors of a point in the full 16,000 dimensional space will be preserved in the 2D embedding.

In [8]:
import umap

# Reduce the dimensionality of the data using UMAP
reducer = umap.UMAP(random_state=0)
X_umap = reducer.fit_transform(X)

# Plot the UMAP embedding
plt.figure(figsize=(8, 8))
plt.scatter(X_umap[:, 0], X_umap[:, 1], c=all_reynolds_numbers)
plt.xlabel("UMAP component 1")
plt.ylabel("UMAP component 2")
Out[8]:
Text(0, 0.5, 'UMAP component 2')
No description has been provided for this image

Can we use our domain knowledge to better separate the data?¶

  • Inductive biases are when we use our problem knowledge to reduce the number of possible learning models

  • Like the bias-variance tradeoff, inductive biases allow us to use domain knowledge to "guide" a model, at the expense of flexibility for different problems

  • For the fluid flow problem, we know that the Navier-Stokes equations contain terms that are quadratic in the velocity field, as well as gradients of the velocity field

  • We will first try using finite time differences to featurize the data, followed by spatial fourier transforms, which implicitly give information about spatial gradients

In [9]:
# Try finite differences
fd1 = np.gradient(all_vorticity_fields, axis=1).reshape((all_vorticity_fields.shape[0], -1))
fd2 = np.gradient(all_vorticity_fields, axis=2).reshape((all_vorticity_fields.shape[0], -1))
X_fd = np.hstack((fd1, fd2))
X_fd = np.reshape(X_fd, (X_fd.shape[0], -1))

## Augment the feature space with finite differences
X_aug = np.concatenate([X, X_fd], axis=1)

# Try PCA and UMAP on the Fourier coefficients

# Reduce the dimensionality of the data using UMAP
reducer = PCA(n_components=2)
X_pca = reducer.fit_transform(X_fd)
plt.figure(figsize=(8, 8))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=all_reynolds_numbers)
plt.xlabel("PCA 1")
plt.ylabel("PCA 2")

reducer = umap.UMAP(random_state=0)
X_umap = reducer.fit_transform(X_fd)
plt.figure(figsize=(8, 8))
plt.scatter(X_umap[:, 0], X_umap[:, 1], c=all_reynolds_numbers)
plt.xlabel("UMAP 1")
plt.ylabel("UMAP 2")
Out[9]:
Text(0, 0.5, 'UMAP 2')
No description has been provided for this image
No description has been provided for this image
In [10]:
## Try featurizing with 2D Fourier coefficients

# Calculate the 2D Fourier coefficients
X_fft = np.fft.fft2(all_vorticity_fields)

# Convert to power spectrum
X_fft = np.reshape(np.abs(X_fft)**2, (X_fft.shape[0], -1))

# Try PCA and UMAP on the Fourier coefficients

# Reduce the dimensionality of the data using UMAP
reducer = PCA(n_components=2)
X_pca = reducer.fit_transform(X_fft)
plt.figure(figsize=(8, 8))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=all_reynolds_numbers)


reducer = umap.UMAP(random_state=0)
X_umap = reducer.fit_transform(X_fft)
plt.figure(figsize=(8, 8))
plt.scatter(X_umap[:, 0], X_umap[:, 1], c=all_reynolds_numbers)
Out[10]:
<matplotlib.collections.PathCollection at 0x3e0c8c210>
No description has been provided for this image
No description has been provided for this image

Let's try training a model to predict Reynolds number¶

  • As a baseline, we'll use multinomial logistic regression, which extends logistic regression to more than two classes

  • Generally, we prefer using a simple model as a baseline, before moving to more complex models

  • In the machine learning literature, baselines and ablations are important for establishing the value of a new model or architecture

In [ ]:
In [34]:
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix

## Shuffle the data and split into training and test sets
sel_inds = np.random.permutation(X.shape[0])[:400]
X_all, y_all = X[sel_inds], y[sel_inds]
X_train, X_test, y_train, y_test = train_test_split(X_all, y_all, test_size=0.4, random_state=0)
# X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=0)


model_logistic = LogisticRegression()
model_logistic.fit(X_train, y_train)
y_pred_logistic = model_logistic.predict(X_test)

print("Training set score: {:.2f}".format(model_logistic.score(X_train, y_train)))
print("Test set score: {:.2f}".format(model_logistic.score(X_test, y_test)))

plt.imshow(confusion_matrix(y_test, y_pred_logistic))
plt.xlabel("Predicted")
plt.ylabel("True")
plt.xticks(np.arange(len(re_vals)), re_vals);
plt.yticks(np.arange(len(re_vals)), re_vals);

Training set score: 1.00
Test set score: 0.62
No description has been provided for this image

A Multilayer Perceptron¶

No description has been provided for this image

Image from Mehta et al. 2018

In [35]:
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=0)

# A 4 layer neural network with 10 hidden units in each layer
mlp = MLPClassifier(hidden_layer_sizes=(3, 3), random_state=0)
mlp.fit(X_train, y_train)
y_pred = mlp.predict(X_test)

print("Training set score: {:.2f}".format(mlp.score(X_train, y_train)))
print("Test set score: {:.2f}".format(mlp.score(X_test, y_test)))

plt.imshow(confusion_matrix(y_test, y_pred))
plt.xlabel("Predicted")
plt.ylabel("True")
plt.xticks(np.arange(len(re_vals)), re_vals);
plt.yticks(np.arange(len(re_vals)), re_vals);

Training set score: 0.89
Test set score: 0.76
No description has been provided for this image

Can we do better? How deep should we go?¶

  • Model choices = hyperparameter tuning. Recall that any "choice" that affects model complexity is a hyperparameter, including the choice of model itself, the optimizer, the learning rate, the number of layers, the number of neurons per layer, the activation function, etc. Here, we will focus on the number and width of layers

  • We use cross-validation (we split train into validation sets)

  • To search over hyperparameters, we use scikit-learn's GridSearchCV, which uses the same API as a standard model, but which internally trains and evaluates the model on all possible hyperparameter combinations with cross-validation

In [43]:
## Tuning hyperparameters with sklearn built-in grid search and cross-validation

from sklearn.model_selection import GridSearchCV

param_grid = {'hidden_layer_sizes': [(3, 3, 3), (5, 5), (7, 5, 3)]}
grid = GridSearchCV(MLPClassifier(), param_grid, cv=5)
grid.fit(X_train, y_train)

print("Best cross-validation score: {:.2f}".format(grid.best_score_))
print("Best parameters: ", grid.best_params_)
print("Test set score: {:.2f}".format(grid.score(X_test, y_test)))

plt.imshow(confusion_matrix(y_test, grid.predict(X_test)))
plt.xlabel("Predicted")
plt.ylabel("True")
plt.xticks(np.arange(len(re_vals)), re_vals);
plt.yticks(np.arange(len(re_vals)), re_vals);

Best cross-validation score: 0.79
Best parameters:  {'hidden_layer_sizes': (5, 5)}
Test set score: 0.83
No description has been provided for this image
In [45]:
## Use the best hyperparameters
mlp = MLPClassifier(**grid.best_params_, random_state=0)
mlp.fit(X_train, y_train)
y_pred_train = mlp.predict(X_train)
y_pred_test = mlp.predict(X_test)

print("Training set score: {:.2f}".format(mlp.score(X_train, y_train)))
print("Test set score: {:.2f}".format(mlp.score(X_test, y_test)))

plt.imshow(confusion_matrix(y_test, y_pred))
plt.xlabel("Predicted")
plt.ylabel("True")
plt.xticks(np.arange(len(re_vals)), re_vals);
plt.yticks(np.arange(len(re_vals)), re_vals);

Training set score: 1.00
Test set score: 0.82
No description has been provided for this image
In [ ]:

Visualize the decision boundary¶

  • Our images live in a high-dimensional feature space, but we can still visualize the decision boundary in a lower-dimensional space using the embedding techniques we learned about last week

  • We will visualize our decision boundary in this embedding space

In [15]:
# Train embedding on the data
reducer = umap.UMAP(random_state=0)
reducer.fit(X)
X_umap_train = reducer.transform(X_train)
X_umap_test = reducer.transform(X_test)

plt.figure(figsize=(8, 8))
plt.scatter(X_umap_train[:, 0], X_umap_train[:, 1], c=y_train)
plt.scatter(X_umap_test[:, 0], X_umap_test[:, 1], c=y_test, marker='o')
plt.xlabel("UMAP 1")
plt.ylabel("UMAP 2")
plt.title("Ground Truth")

plt.figure(figsize=(8, 8))
plt.scatter(X_umap_train[:, 0], X_umap_train[:, 1], c=y_pred_train)
plt.scatter(X_umap_test[:, 0], X_umap_test[:, 1], c=y_pred_test, marker='o')
plt.xlabel("UMAP 1")
plt.ylabel("UMAP 2")
plt.title("Multi-Layer Perceptron")

plt.figure(figsize=(8, 8))
# plt.scatter(X_umap_train[:, 0], X_umap_train[:, 1], c=y_train)
# plt.scatter(X_umap_test[:, 0], X_umap_test[:, 1], c=y_pred_logistic, marker='o')
# plt.xlabel("UMAP 1")
# plt.ylabel("UMAP 2")
# plt.title("Logistic Regression")
Out[15]:
<Figure size 800x800 with 0 Axes>
No description has been provided for this image
No description has been provided for this image 
<Figure size 800x800 with 0 Axes>

How big is our model?¶

  • Our final neural network maps from $127^2 = 16,129$ features to 4 classes, with 1 hidden layers containing 10 neurons

  • This means we have around 160,000 trainable parameters

In [40]:
grid.best_params_
Out[40]:
{'hidden_layer_sizes': (7,)}

A convolutional neural network¶

  • Can we process the images in a more parameter-efficient way?

  • The Multi-Layer oerceptron model we used above has a lot of trainable parameters, since it maps flattened images that have $127^2 = 16129$ features into a single output. Even a linear model would have 16129 parameters!

  • We know that turbulent flows have a lot of spatial structure, and that the Navier-Stokes equations are local in space. Can we build this property into our model?

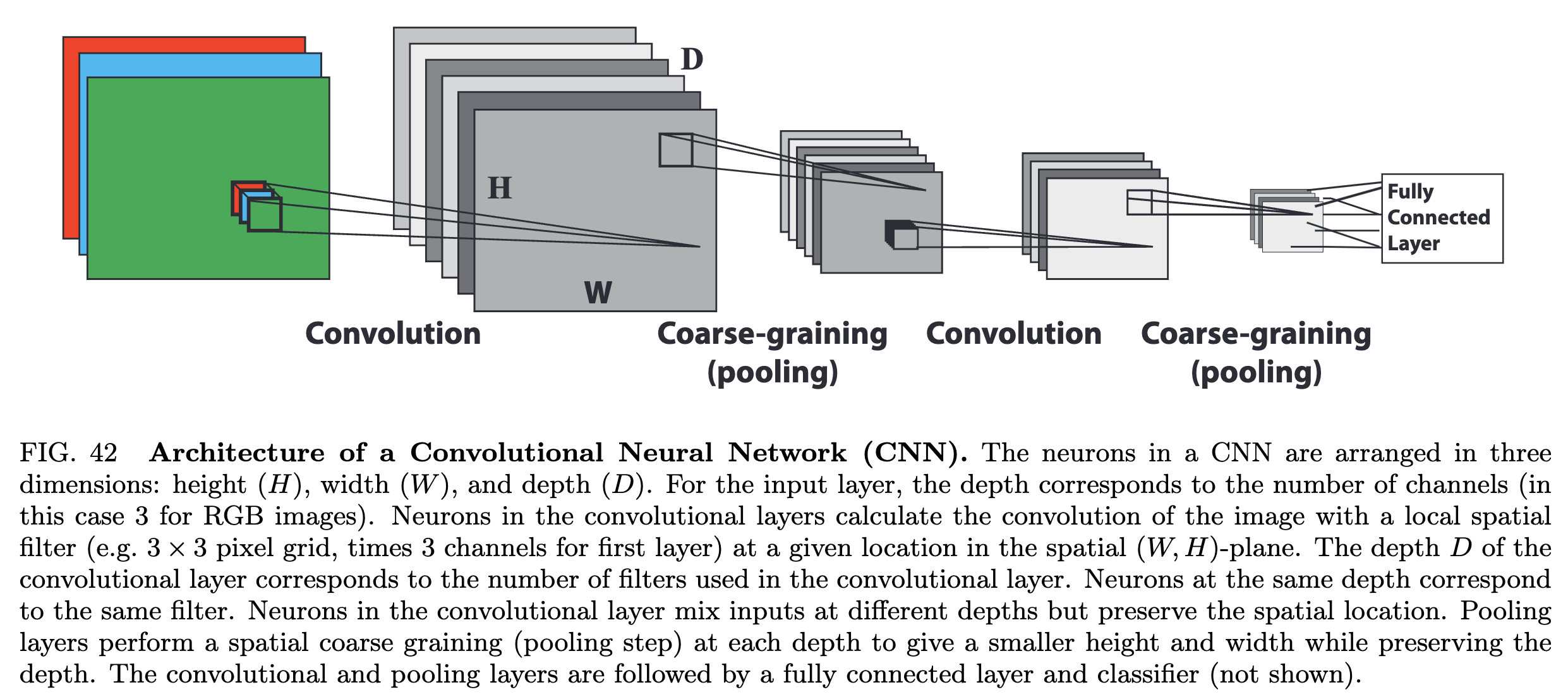
No description has been provided for this image

Image from Mehta et al. 2018

  • In a convolutional neural network (CNN), we avoid explicitly flattening the image, and instead apply a series of trainable convolutional filters to the image

  • Recall that convolutional filters are usually small kernels, like $3 \times 3$ or $5 \times 5$ images, that we slide across the image. The output of a discrete convolution is a new image, where each pixel is a combination of pixel neighborhoods from the previous image

  • Our image classifier needs to map from an image to a single output, and so CNN also includes a series of pooling layers, which downsample the intermediate images

  • After the image becomes sufficiently small, we then flatten it and apply a standard fully-connected neural network to the flattened image

In [ ]:
  • As a starting point, we will leave our input dataset in the form of images. So instead of our training data having the shape $X \in \mathbb{R}^{N_\text{data} \times N_\text{feats}}$, it will have the shape $X \in \mathbb{R}^{N_\text{data} \times N_\text{pixels} \times N_\text{pixels}}$
In [18]:
## Convert into a machine-learning dataset by flattening features

X = np.copy(all_vorticity_fields)[..., None]
# Standardize the data
X = (X - np.mean(X, axis=0)) / np.std(X, axis=0)
y = np.unique(all_reynolds_numbers, return_inverse=True)[1] # Convert labels to integers


from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=0)


print("Training data has shape: {}".format(X_train.shape))
print("Training labels have shape: {}".format(y_train.shape))

print("Test data has shape: {}".format(X_test.shape))
print("Test labels have shape: {}".format(y_test.shape))


plt.hist(y_train)
plt.xlabel("Class")
plt.ylabel("Count")

Training data has shape: (1200, 127, 127, 1)
Training labels have shape: (1200,)
Test data has shape: (800, 127, 127, 1)
Test labels have shape: (800,)
Out[18]:
Text(0, 0.5, 'Count')
No description has been provided for this image

  • We will now implement a CNN using JAX, a library for automatic differentiation and GPU acceleration

  • Our implementation will inherit structure from scikit-learn, so that we can use the same fit and predict API as before

In [ ]:
import jax
import jax.numpy as jnp
from jax import grad, jit, random, value_and_grad
import optax # An optimization library for JAX
from sklearn.base import BaseEstimator, ClassifierMixin

class CNNClassifier(BaseEstimator, ClassifierMixin):
    """
    A Convolutional Neural Network (CNN) classifier implemented using JAX and NumPy.

    Parameters:
        learning_rate (float): The learning rate for the optimizer
        epochs (int): The number of training epochs
        batch_size (int): The batch size for training
        random_state (int): The random seed for reproducibility


    """
    def __init__(self, learning_rate=0.001, epochs=10, batch_size=32, random_state=0, store_history=True):

        ## Set hyperparameters
        self.learning_rate = learning_rate
        self.epochs = epochs
        self.batch_size = batch_size

        ## Set trainable parameters and internal object state
        self.params = None
        self.opt_state = None

        self.random_state = random_state
        # JAX uses PRNG objects to control random number generation
        self.rng = random.PRNGKey(random_state) 

        self.store_history = store_history
        if self.store_history:
            self.loss_history = []


    def _init_params(self, input_shape, num_classes):
        """
        Initialize the model parameters

        Args:
            input_shape (tuple): The shape of the input data
            num_classes (int): The number of classes in the classification task

        Returns:
            None
        
        """
        self.params = {
            "conv1": {
                "w": random.normal(self.rng, (3, 3, input_shape[-1], 32)),
                "b": jnp.zeros((32,))
            },
            "fc": {
                "w": random.normal(self.rng, (32 * (input_shape[0] // 2) * (input_shape[1] // 2), num_classes)),
                "b": jnp.zeros((num_classes,))
            }
        }

    def _forward(self, params, X):
        """
        Forward pass of the CNN model. Given a batch of data, compute the logits
        corresponding to each class.

        Args:
            params (dict): Dictionary containing the model parameters
            X (numpy.ndarray): Batch of input data

        Returns:
            numpy.ndarray: Logits for each class
        """
        def relu(x):
            return jnp.maximum(0, x)

        # Convolution layer transforms the input image from a shape of 
        # (batch_size, height, width, channels), here (64, 128, 128, 1), to a shape of
        # (batch_size, height, width, num_filters), here (64, 128, 128, 32)
        conv1_out = jax.lax.conv_general_dilated(
            X,
            params["conv1"]["w"],
            window_strides=(1, 1),
            dimension_numbers=("NHWC", "HWIO", "NHWC"),
            padding="SAME"
        )
        conv1_out = relu(conv1_out + params["conv1"]["b"])

        # Pooling layer shrinks the intermediate representation to
        # (batch_size, height // 2, width // 2, num_filters), here (64, 64, 64, 32)
        pool_out = jax.lax.reduce_window(
            conv1_out,
            0.0,
            jax.lax.add,
            window_dimensions=(1, 2, 2, 1),
            window_strides=(1, 2, 2, 1),
            padding="VALID"
        )

        # The flattening operation reshapes the tensor to (batch_size, num_features),
        # here (64, 64 * 64 * 32), and then computes the logits
        flattened = pool_out.reshape((X.shape[0], -1))
        logits = jnp.dot(flattened, params["fc"]["w"]) + params["fc"]["b"]

        return logits

    def _loss(self, params, X, y):
        """
        Compute the cross-entropy loss between the model predictions and the true labels

        The cross-entropy loss is defined as:

        L = -1/N * sum_i sum_j y_ij * log(p_ij)

        where N is the number of samples, y_ij is 1 if sample i belongs to class j, and p_ij
        is the predicted probability that sample i belongs to class j.

        Args:
            params (dict): Dictionary containing the model parameters
            X (numpy.ndarray): Batch of input data
            y (numpy.ndarray): Batch of labels

        Returns:
            numpy.ndarray: The cross-entropy loss, averaged over the batch
        """
        logits = self._forward(params, X)
        y_onehot = jax.nn.one_hot(y, logits.shape[-1])
        loss = -jnp.mean(jnp.sum(y_onehot * jax.nn.log_softmax(logits), axis=-1))
        return loss

    def _update(self, params, opt_state, X, y):
        """
        Compute the gradients of the loss with respect to the model parameters and 
        update the model

        Args:
            params (dict): Dictionary containing the model parameters
            opt_state (dict): Dictionary containing the optimizer state
            X (numpy.ndarray): Batch of input data
            y (numpy.ndarray): Batch of labels

        Returns:
            dict: Updated model parameters
            dict: Updated optimizer state
            float: The loss value
        """
        loss, grads = value_and_grad(self._loss)(params, X, y)
        updates, opt_state = self.optimizer.update(grads, opt_state, params)
        params = optax.apply_updates(params, updates)
        return params, opt_state, loss

    def fit(self, X, y):
        """
        Fit the CNN model to the training data

        Args:
            X (numpy.ndarray): Training data of shape (num_samples, height, width, channels)
            y (numpy.ndarray): Training labels of shape (num_samples,)
        """

        ## Initialize the model parameters and optimizer at the first call to fit
        if self.params is None:
            input_shape = X.shape[1:]
            num_classes = len(jnp.unique(y))
            self._init_params(input_shape, num_classes)
            self.optimizer = optax.adam(self.learning_rate)
            self.opt_state = self.optimizer.init(self.params)

        ## Optimization loop
        for epoch in range(self.epochs):
            perm = random.permutation(self.rng, X.shape[0])
            X, y = X[perm], y[perm]
            for i in range(0, X.shape[0], self.batch_size):
                X_batch = X[i:i + self.batch_size]
                y_batch = y[i:i + self.batch_size]
                self.params, self.opt_state, loss = self._update(self.params, self.opt_state, X_batch, y_batch)
            if self.store_history:
                self.loss_history.append(loss)
                print(f"Epoch {epoch + 1}/{self.epochs}, Loss: {loss:.4f}")

    def predict(self, X):
        """
        Make predictions on new data

        Args:
            X (numpy.ndarray): New data of shape (num_samples, height, width, channels) 

        Returns:
            numpy.ndarray: Predicted labels
        """
        logits = self._forward(self.params, X)
        return jnp.argmax(logits, axis=-1)
In [30]:
## Fit the CNN model

# # Train and predict
model = CNNClassifier(learning_rate=0.0001, epochs=100, batch_size=16)
model.fit(X_train, y_train)


plt.plot(model.loss_history)
plt.xlabel("Epoch")
plt.ylabel("Cross-entropy loss on training set")

Epoch 1/100, Loss: 2344.1562
Epoch 2/100, Loss: 1893.5312
Epoch 3/100, Loss: 2167.5793
Epoch 4/100, Loss: 1665.8159
Epoch 5/100, Loss: 1502.6653
Epoch 6/100, Loss: 948.9930
Epoch 7/100, Loss: 1231.2178
Epoch 8/100, Loss: 1153.6851
Epoch 9/100, Loss: 929.2589
Epoch 10/100, Loss: 652.1995
Epoch 11/100, Loss: 492.6980
Epoch 12/100, Loss: 784.1656
Epoch 13/100, Loss: 455.9197
Epoch 14/100, Loss: 227.0690
Epoch 15/100, Loss: 274.9376
Epoch 16/100, Loss: 538.9522
Epoch 17/100, Loss: 682.2462
Epoch 18/100, Loss: 94.5268
Epoch 19/100, Loss: 242.6960
Epoch 20/100, Loss: 158.2983
Epoch 21/100, Loss: 236.4017
Epoch 22/100, Loss: 401.7467
Epoch 23/100, Loss: 113.3213
Epoch 24/100, Loss: 195.1394
Epoch 25/100, Loss: 117.2153
Epoch 26/100, Loss: 113.0649
Epoch 27/100, Loss: 261.6731
Epoch 28/100, Loss: 215.6727
Epoch 29/100, Loss: 132.2099
Epoch 30/100, Loss: 216.4857
Epoch 31/100, Loss: 127.0312
Epoch 32/100, Loss: 17.0016
Epoch 33/100, Loss: 165.9627
Epoch 34/100, Loss: 63.9287
Epoch 35/100, Loss: 151.2602
Epoch 36/100, Loss: -0.0000
Epoch 37/100, Loss: -0.0000
Epoch 38/100, Loss: 271.1634
Epoch 39/100, Loss: -0.0000
Epoch 40/100, Loss: -0.0000
Epoch 41/100, Loss: -0.0000
Epoch 42/100, Loss: 44.3639
Epoch 43/100, Loss: 0.5360
Epoch 44/100, Loss: 63.3394
Epoch 45/100, Loss: -0.0000
Epoch 46/100, Loss: 4.4885
Epoch 47/100, Loss: 11.2855
Epoch 48/100, Loss: -0.0000
Epoch 49/100, Loss: -0.0000
Epoch 50/100, Loss: 46.8023
Epoch 51/100, Loss: 2.0290
Epoch 52/100, Loss: -0.0000
Epoch 53/100, Loss: 6.1905
Epoch 54/100, Loss: 4.0004
Epoch 55/100, Loss: -0.0000
Epoch 56/100, Loss: -0.0000
Epoch 57/100, Loss: -0.0000
Epoch 58/100, Loss: -0.0000
Epoch 59/100, Loss: -0.0000
Epoch 60/100, Loss: 27.7790
Epoch 61/100, Loss: -0.0000
Epoch 62/100, Loss: -0.0000
Epoch 63/100, Loss: -0.0000
Epoch 64/100, Loss: -0.0000
Epoch 65/100, Loss: -0.0000
Epoch 66/100, Loss: -0.0000
Epoch 67/100, Loss: -0.0000
Epoch 68/100, Loss: 0.0001
Epoch 69/100, Loss: -0.0000
Epoch 70/100, Loss: -0.0000
Epoch 71/100, Loss: 0.8741
Epoch 72/100, Loss: -0.0000
Epoch 73/100, Loss: -0.0000
Epoch 74/100, Loss: -0.0000
Epoch 75/100, Loss: -0.0000
Epoch 76/100, Loss: -0.0000
Epoch 77/100, Loss: -0.0000
Epoch 78/100, Loss: -0.0000
Epoch 79/100, Loss: -0.0000
Epoch 80/100, Loss: -0.0000
Epoch 81/100, Loss: -0.0000
Epoch 82/100, Loss: -0.0000
Epoch 83/100, Loss: -0.0000
Epoch 84/100, Loss: -0.0000
Epoch 85/100, Loss: -0.0000
Epoch 86/100, Loss: -0.0000
Epoch 87/100, Loss: -0.0000
Epoch 88/100, Loss: -0.0000
Epoch 89/100, Loss: -0.0000
Epoch 90/100, Loss: -0.0000
Epoch 91/100, Loss: -0.0000
Epoch 92/100, Loss: -0.0000
Epoch 93/100, Loss: -0.0000
Epoch 94/100, Loss: -0.0000
Epoch 95/100, Loss: -0.0000
Epoch 96/100, Loss: -0.0000
Epoch 97/100, Loss: -0.0000
Epoch 98/100, Loss: -0.0000
Epoch 99/100, Loss: -0.0000
Epoch 100/100, Loss: -0.0000
Out[30]:
Text(0, 0.5, 'Cross-entropy loss on training set')
No description has been provided for this image
In [31]:
y_pred_train = model.predict(X_train)
y_pred_test = model.predict(X_test)

print("Training set score: {:.2f}".format(np.mean(y_pred_train == y_train)))
print("Test set score: {:.2f}".format(np.mean(y_pred_test == y_test)))

plt.imshow(confusion_matrix(y_test, y_pred_test))
plt.xlabel("Predicted")
plt.ylabel("True")
plt.xticks(np.arange(len(re_vals)), re_vals);
plt.yticks(np.arange(len(re_vals)), re_vals);

Training set score: 1.00
Test set score: 0.78
No description has been provided for this image

How many parameters did that take?¶

  • The convolutional layer has $N_\text{filters} \times N_\text{pixels} \times N_\text{pixels} \times N_\text{channels}$ parameters. In our case, $N_\text{filters} = 16$, $N_\text{pixels} = 127$, $N_\text{channels} = 1$

  • The fully connected layer has $N_\text{filters} \times N_\text{pixels} \times N_\text{pixels} \times N_\text{channels} \times N_\text{neurons}$ parameters. In our case, $N_\text{neurons} = 2$

  • The total number of parameters is therefore $16 \times 127 \times 127 + 16 \times 2 = 325,858$

In [91]:
model.params['conv1']['w'].shape
Out[91]:
(3, 3, 1, 32)
In [96]:
model.params['fc']['w'].shape
Out[96]:
(127008, 4)
In [ ]:
In [ ]:

Inductive biases in machine learning¶

  • By using a CNN, we managed to get both higher accuracy and lower number of parameters

  • This is because the CNN architecture has inductive biase for datasets with spatial translation invariance

  • There's no free lunch: the CNN architecture is not as flexible as the MLP, and so it may not work as well on other datasets. But because our dataset has spatial structure, we can exploit this to get better performance

  • We can see this as a vignette of our role as physicists using machine learning: we can use our domain knowledge to guide our model choices, and to get better performance with fewer parameters. But this comes at the expense of flexibility for other datasets.

  • Currently, as of 2024, the "bitter lesson" of machine learning has been that domain-specific inductive biases become unnecessary as models become larger and trained on more data. As a result, advances in bioinformatics and language have been possible with models with relatively little domain-specific knowledge.

In [ ]:
mlp.fit(X_train, y_train)
y_pred_train = mlp.predict(X_train)
y_pred_test = mlp.predict(X_test)

print("Training set score: {:.2f}".format(mlp.score(X_train, y_train)))
print("Test set score: {:.2f}".format(mlp.score(X_test, y_test)))
In [ ]: